[ML101] Chương 7: Giảm chiều dữ liệu (Dimensionality Reduction)

Bài viết có tham khảo, sử dụng và sửa đổi tài nguyên từ kho lưu trữ handson-mlp, tuân thủ giấy phép Apache‑2.0. Chúng tôi chân thành cảm ơn tác giả Aurélien Géron (@aureliengeron) vì sự chia sẻ kiến thức tuyệt vời và những đóng góp quý giá cho cộng đồng.

Nhiều bài toán Học máy (Machine Learning) liên quan đến việc huấn luyện trên hàng ngàn, thậm chí hàng triệu đặc trưng (features) cho mỗi mẫu dữ liệu. Việc này không chỉ khiến quá trình huấn luyện trở nên cực kỳ chậm chạp mà còn làm cho việc tìm ra giải pháp tối ưu trở nên khó khăn hơn rất nhiều. Vấn đề này thường được gọi là Lời nguyền của số chiều (Curse of Dimensionality).

May mắn thay, trong các bài toán thực tế, chúng ta thường có thể giảm số lượng đặc trưng đáng kể, biến một bài toán khó giải thành bài toán dễ giải hơn mà không làm mất đi quá nhiều thông tin quan trọng. Ngoài việc tăng tốc độ huấn luyện, Giảm chiều dữ liệu (Dimensionality Reduction) còn cực kỳ hữu ích cho việc trực quan hóa dữ liệu (data visualization). Giảm số chiều xuống còn 2 hoặc 3 cho phép chúng ta vẽ dữ liệu lên biểu đồ, từ đó có thể quan sát trực quan các cụm (clusters) hoặc các mẫu (patterns) quan trọng.

Trong chương này, chúng ta sẽ tìm hiểu hai phương pháp chính để giảm chiều dữ liệu: Phép chiếu (Projection) và Học đa tạp (Manifold Learning), cùng với các thuật toán phổ biến như PCA, Kernel PCA và LLE.

Bạn có thể chạy trực tiếp các đoạn mã code tại: Google Colab.

Cài đặt môi trường

Dự án này yêu cầu Python 3.10 trở lên và thư viện Scikit-Learn phiên bản từ 1.6.1 trở lên. Giống như các chương trước, đoạn mã dưới đây dùng để kiểm tra các yêu cầu này và thiết lập cấu hình hiển thị cho các biểu đồ.

import sys

# Kiểm tra phiên bản Python phải từ 3.10 trở lên
assert sys.version_info >= (3, 10)

from packaging.version import Version
import sklearn

# Kiểm tra phiên bản Scikit-Learn phải từ 1.6.1 trở lên
assert Version(sklearn.__version__) >= Version("1.6.1")

# Thiết lập kích thước font chữ mặc định cho biểu đồ matplotlib để dễ nhìn hơn
import matplotlib.pyplot as plt

plt.rc('font', size=14)
plt.rc('axes', labelsize=14, titlesize=14)
plt.rc('legend', fontsize=14)
plt.rc('xtick', labelsize=10)
plt.rc('ytick', labelsize=10)

Phân tích thành phần chính (PCA)

Phân tích thành phần chính (Principal Component Analysis - PCA) là thuật toán giảm chiều dữ liệu phổ biến nhất hiện nay. Nguyên lý cơ bản của PCA là xác định một siêu phẳng (hyperplane) nằm gần dữ liệu nhất, sau đó chiếu dữ liệu lên siêu phẳng này.

Trước khi đi sâu vào thuật toán, chúng ta sẽ tạo một vài hình ảnh minh họa để hiểu rõ hơn về khái niệm PCA và Học đa tạp. Bạn có thể bỏ qua phần tạo dữ liệu giả lập dưới đây và đi thẳng đến phần lý thuyết PCA nếu muốn.

Đầu tiên, chúng ta sẽ tạo ra một tập dữ liệu 3D nhỏ. Tập dữ liệu này có hình dạng bầu dục, được xoay trong không gian 3D, các điểm phân bố không đều và có chứa nhiễu (noise).

# extra code - Đoạn mã này dùng để tạo dữ liệu giả lập
import numpy as np
from scipy.spatial.transform import Rotation

m = 60 # Số lượng mẫu dữ liệu
X = np.zeros((m, 3))  # Khởi tạo tập dữ liệu 3D với toàn số 0
rng = np.random.default_rng(seed=42) # Khởi tạo bộ sinh số ngẫu nhiên

# Tạo phân bố không đều cho các góc
angles = (rng.random(m) ** 3 + 0.5) * 2 * np.pi

# Tạo hình bầu dục (oval) dựa trên hàm cos và sin
X[:, 0], X[:, 1] = np.cos(angles), np.sin(angles) * 0.5

# Thêm nhiễu (noise) vào dữ liệu
X += 0.28 * rng.standard_normal((m, 3))

# Xoay dữ liệu trong không gian 3D
X = Rotation.from_rotvec([np.pi / 29, -np.pi / 20, np.pi / 4]).apply(X)

# Dịch chuyển dữ liệu đi một chút
X += [0.2, 0, 0.2]

Tiếp theo, chúng ta sẽ vẽ tập dữ liệu 3D này cùng với mặt phẳng chiếu (projection plane). Hình ảnh này giúp hình dung cách PCA tìm ra mặt phẳng tối ưu để chiếu dữ liệu lên đó nhằm giữ lại nhiều thông tin (phương sai) nhất có thể.

# extra code – ô này tạo ra Hình 7–2
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

pca = PCA(n_components=2) # Khởi tạo PCA để giảm xuống 2 chiều
X2D = pca.fit_transform(X)  # Thực hiện giảm chiều dữ liệu
X3D_inv = pca.inverse_transform(X2D)  # Tái tạo lại vị trí 3D từ dữ liệu đã chiếu

# Tính toán để vẽ mặt phẳng chiếu
X_centered = X - X.mean(axis=0)
U, s, Vt = np.linalg.svd(X_centered)
axes = [-1.4, 1.4, -1.4, 1.4, -1.1, 1.1]
x1, x2 = np.meshgrid(np.linspace(axes[0], axes[1], 10),
                     np.linspace(axes[2], axes[3], 10))
w1, w2 = np.linalg.solve(Vt[:2, :2], Vt[:2, 2])  # Hệ số mặt phẳng chiếu
z = w1 * (x1 - pca.mean_[0]) + w2 * (x2 - pca.mean_[1]) - pca.mean_[2]  # Mặt phẳng

# Phân loại các điểm nằm trên và dưới mặt phẳng để vẽ cho đẹp
X3D_above = X[X[:, 2] >= X3D_inv[:, 2]]
X3D_below = X[X[:, 2] < X3D_inv[:, 2]]

fig = plt.figure(figsize=(9, 9))
ax = fig.add_subplot(111, projection="3d")

# Vẽ các điểm và đường chiếu nằm dưới mặt phẳng trước
ax.plot(X3D_below[:, 0], X3D_below[:, 1], X3D_below[:, 2], "ro", alpha=0.3)
for i in range(m):
    if X[i, 2] < X3D_inv[i, 2]:
        ax.plot([X[i][0], X3D_inv[i][0]],
                [X[i][1], X3D_inv[i][1]],
                [X[i][2], X3D_inv[i][2]], ":", color="#F88")

ax.plot_surface(x1, x2, z, alpha=0.1, color="b")  # Vẽ mặt phẳng chiếu
ax.plot(X3D_inv[:, 0], X3D_inv[:, 1], X3D_inv[:, 2], "b+")  # Các điểm đã chiếu
ax.plot(X3D_inv[:, 0], X3D_inv[:, 1], X3D_inv[:, 2], "b.")

# Bây giờ vẽ các đường chiếu và điểm nằm trên mặt phẳng
for i in range(m):
    if X[i, 2] >= X3D_inv[i, 2]:
        ax.plot([X[i][0], X3D_inv[i][0]],
                [X[i][1], X3D_inv[i][1]],
                [X[i][2], X3D_inv[i][2]], "r--")

ax.plot(X3D_above[:, 0], X3D_above[:, 1], X3D_above[:, 2], "ro")

def set_xyz_axes(ax, axes):
    ax.xaxis.set_rotate_label(False)
    ax.yaxis.set_rotate_label(False)
    ax.zaxis.set_rotate_label(False)
    ax.set_xlabel("$x_1$", labelpad=8, rotation=0)
    ax.set_ylabel("$x_2$", labelpad=8, rotation=0)
    ax.set_zlabel("$x_3$", labelpad=8, rotation=0)
    ax.set_xlim(axes[0:2])
    ax.set_ylim(axes[2:4])
    ax.set_zlim(axes[4:6])

set_xyz_axes(ax, axes)
ax.set_zticks([-1, -0.5, 0, 0.5, 1])
plt.show()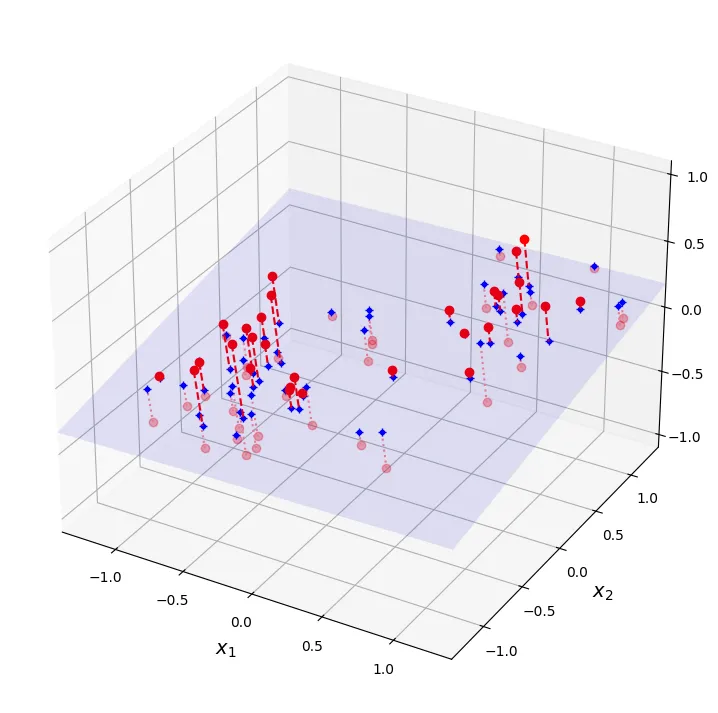

Hình ảnh dưới đây minh họa kết quả sau khi chiếu tập dữ liệu 3D xuống không gian 2D. Lưu ý rằng PCA bảo toàn phương sai tốt nhất có thể, giúp cấu trúc của dữ liệu được giữ lại rõ ràng.

# extra code – ô này tạo ra Hình 7–3 (Kết quả chiếu 2D)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1, aspect='equal')
ax.plot(X2D[:, 0], X2D[:, 1], "b+")
ax.plot(X2D[:, 0], X2D[:, 1], "b.")
ax.plot([0], [0], "bo")
ax.arrow(0, 0, 1, 0, head_width=0.05, length_includes_head=True,
         head_length=0.1, fc='b', ec='b', linewidth=4)
ax.arrow(0, 0, 0, 1, head_width=0.05, length_includes_head=True,
         head_length=0.1, fc='b', ec='b', linewidth=1)
ax.set_xlabel("$z_1$")
ax.set_yticks([-0.5, 0, 0.5, 1])
ax.set_ylabel("$z_2$", rotation=0)
ax.set_axisbelow(True)
ax.grid(True)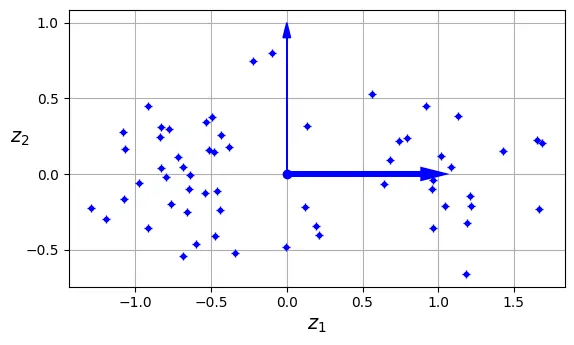

Học đa tạp (Manifold Learning)

Không phải lúc nào phép chiếu cũng là phương pháp tốt nhất. Ví dụ điển hình là tập dữ liệu Swiss Roll (bánh cuộn Thụy Sĩ). Đây là một tập dữ liệu 3D bị cuộn tròn lại. Nếu chúng ta dùng phép chiếu (Projection) thông thường (như PCA), các lớp của cuộn bánh sẽ bị đè lên nhau, làm mất cấu trúc dữ liệu.

Mục tiêu của Manifold Learning là “mở cuộn” (unroll) hoặc trải phẳng đa tạp này ra không gian thấp chiều hơn mà vẫn giữ được cấu trúc lân cận cục bộ.

from sklearn.datasets import make_swiss_roll

# Tạo dữ liệu Swiss roll
X_swiss, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=42)

# extra code – ô này tạo ra Hình 7–4 (Hiển thị Swiss roll 3D)
from matplotlib.colors import ListedColormap

darker_hot = ListedColormap(plt.cm.hot(np.linspace(0, 0.8, 256)))
axes = [-11.5, 14, -2, 23, -12, 15]

fig = plt.figure(figsize=(6, 5))
ax = fig.add_subplot(111, projection='3d')

ax.scatter(X_swiss[:, 0], X_swiss[:, 1], X_swiss[:, 2], c=t, cmap=darker_hot)
ax.view_init(10, -70)
set_xyz_axes(ax, axes)
plt.show()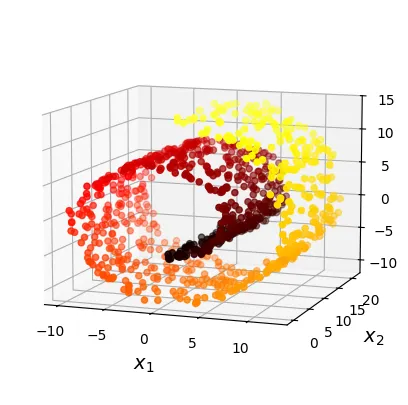

Dưới đây là so sánh giữa việc chiếu dữ liệu (Projection) và việc trải phẳng đa tạp (Manifold Unrolling).

Bên trái là kết quả của việc chiếu thẳng xuống mặt phẳng: các điểm màu khác nhau bị trộn lẫn (squashing). Bên phải là kết quả mong muốn của việc “mở cuộn”: các điểm màu được trải ra theo đúng trật tự của chúng.

# extra code – ô này tạo các biểu đồ cho Hình 7–5
plt.figure(figsize=(10, 4))

plt.subplot(121)
plt.scatter(X_swiss[:, 0], X_swiss[:, 1], c=t, cmap=darker_hot)
plt.axis(axes[:4])
plt.xlabel("$x_1$")
plt.ylabel("$x_2$", labelpad=10, rotation=0)
plt.grid(True)

plt.subplot(122)
plt.scatter(t, X_swiss[:, 1], c=t, cmap=darker_hot)
plt.axis([4, 14.8, axes[2], axes[3]])
plt.xlabel("$z_1$")
plt.grid(True)
plt.show()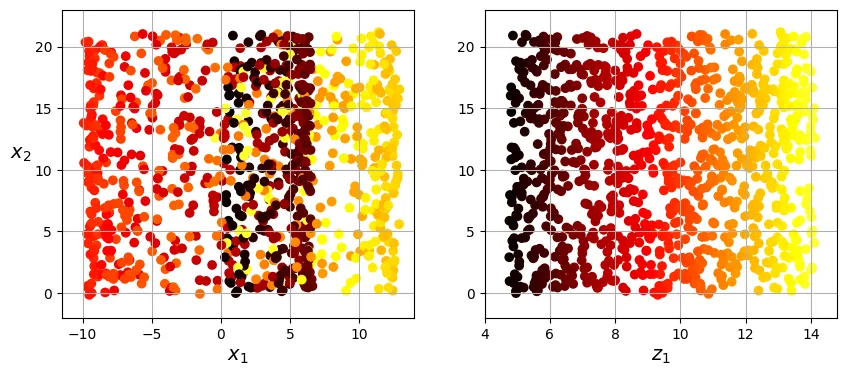

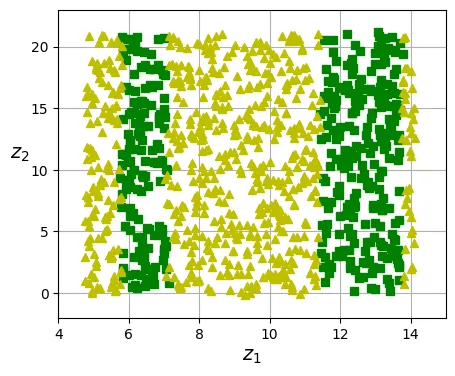
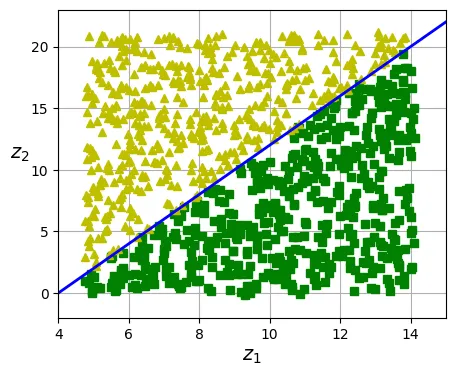
Hình dưới đây minh họa sự khác biệt trong đường biên quyết định (decision boundary) khi xử lý dữ liệu phức tạp. Nếu chúng ta cố gắng phân lớp trực tiếp trên không gian 3D (ví dụ cắt bằng một mặt phẳng), kết quả sẽ không tốt. Tuy nhiên, nếu chúng ta giảm chiều dữ liệu một cách hợp lý (mở cuộn), bài toán phân lớp trở nên đơn giản hơn nhiều.

# extra code – ô này tạo các biểu đồ cho Hình 7–6
axes = [-11.5, 14, -2, 23, -12, 15]
x2s = np.linspace(axes[2], axes[3], 10)
x3s = np.linspace(axes[4], axes[5], 10)
x2, x3 = np.meshgrid(x2s, x3s)

# Trường hợp 1: Phân lớp dựa trên tọa độ không gian 3D gốc
positive_class = X_swiss[:, 0] > 5
X_pos = X_swiss[positive_class]
X_neg = X_swiss[~positive_class]

fig = plt.figure(figsize=(6, 5))
ax = plt.subplot(1, 1, 1, projection='3d')
ax.view_init(10, -70)
ax.plot(X_neg[:, 0], X_neg[:, 1], X_neg[:, 2], "y^")
ax.plot_wireframe(5, x2, x3, alpha=0.5)
ax.plot(X_pos[:, 0], X_pos[:, 1], X_pos[:, 2], "gs")
set_xyz_axes(ax, axes)
plt.show()

fig = plt.figure(figsize=(5, 4))
ax = plt.subplot(1, 1, 1)
ax.plot(t[positive_class], X_swiss[positive_class, 1], "gs")
ax.plot(t[~positive_class], X_swiss[~positive_class, 1], "y^")
ax.axis([4, 15, axes[2], axes[3]])
ax.set_xlabel("$z_1$")
ax.set_ylabel("$z_2$", rotation=0, labelpad=8)
ax.grid(True)
plt.show()

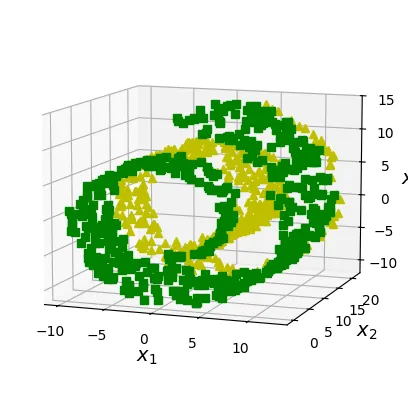
# Trường hợp 2: Phân lớp dựa trên tọa độ đã được mở cuộn (manifold)
positive_class = 2 * (t[:] - 4) > X_swiss[:, 1]
X_pos = X_swiss[positive_class]
X_neg = X_swiss[~positive_class]

fig = plt.figure(figsize=(6, 5))
ax = plt.subplot(1, 1, 1, projection='3d')
ax.view_init(10, -70)
ax.plot(X_neg[:, 0], X_neg[:, 1], X_neg[:, 2], "y^")
ax.plot(X_pos[:, 0], X_pos[:, 1], X_pos[:, 2], "gs")
ax.xaxis.set_rotate_label(False)
ax.yaxis.set_rotate_label(False)
ax.zaxis.set_rotate_label(False)
ax.set_xlabel("$x_1$", rotation=0)
ax.set_ylabel("$x_2$", rotation=0)
ax.set_zlabel("$x_3$", rotation=0)
ax.set_xlim(axes[0:2])
ax.set_ylim(axes[2:4])
ax.set_zlim(axes[4:6])
plt.show()

fig = plt.figure(figsize=(5, 4))
ax = plt.subplot(1, 1, 1)
ax.plot(t[positive_class], X_swiss[positive_class, 1], "gs")
ax.plot(t[~positive_class], X_swiss[~positive_class, 1], "y^")
ax.plot([4, 15], [0, 22], "b-", linewidth=2)
ax.axis([4, 15, axes[2], axes[3]])
ax.set_xlabel("$z_1$")
ax.set_ylabel("$z_2$", rotation=0, labelpad=8)
ax.grid(True)
plt.show()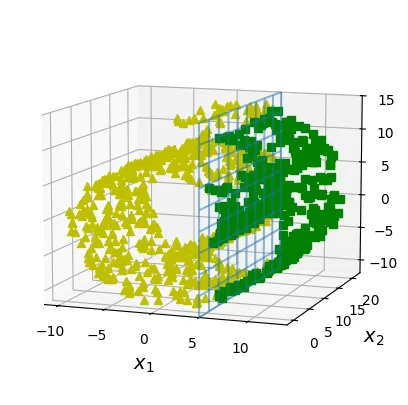

Một khái niệm quan trọng trong PCA là việc chọn trục chiếu nào giữ lại nhiều thông tin nhất. “Thông tin” ở đây được đo lường bằng phương sai (variance). Trục nào làm cho dữ liệu trải rộng ra nhất (phương sai lớn nhất) sẽ là trục chứa nhiều thông tin nhất.

Hình dưới đây minh họa việc chọn trục chiếu. $c_1$ là trục có phương sai lớn nhất, $c_2$ vuông góc với $c_1$. Nếu chiếu lên $c_1$, các điểm đỏ phân tán rộng (tốt). Nếu chiếu lên $c_2$, các điểm đỏ co cụm lại (mất thông tin).

# extra code – ô này tạo ra Hình 7–7 (Chọn thành phần chính)
angle = np.pi / 5
stretch = 5
m = 200
rng = np.random.default_rng(seed=3)
X_line = rng.standard_normal((m, 2)) / 10
X_line = X_line @ np.array([[stretch, 0], [0, 1]])  # Kéo dãn dữ liệu
X_line = X_line @ [[np.cos(angle), np.sin(angle)],
                   [np.sin(angle), np.cos(angle)]]  # Xoay dữ liệu

u1 = np.array([np.cos(angle), np.sin(angle)])
u2 = np.array([np.cos(angle - 2 * np.pi / 6), np.sin(angle - 2 * np.pi / 6)])
u3 = np.array([np.cos(angle - np.pi / 2), np.sin(angle - np.pi / 2)])

X_proj1 = X_line @ u1.reshape(-1, 1)
X_proj2 = X_line @ u2.reshape(-1, 1)
X_proj3 = X_line @ u3.reshape(-1, 1)

plt.figure(figsize=(8, 4))
plt.subplot2grid((3, 2), (0, 0), rowspan=3)
plt.plot([-1.4, 1.4], [-1.4 * u1[1] / u1[0], 1.4 * u1[1] / u1[0]], "k-",
         linewidth=2)
plt.plot([-1.4, 1.4], [-1.4 * u2[1] / u2[0], 1.4 * u2[1] / u2[0]], "k--",
         linewidth=2)
plt.plot([-1.4, 1.4], [-1.4 * u3[1] / u3[0], 1.4 * u3[1] / u3[0]], "k:",
         linewidth=2)
plt.plot(X_line[:, 0], X_line[:, 1], "ro", alpha=0.5)
plt.arrow(0, 0, u1[0], u1[1], head_width=0.1, linewidth=4, alpha=0.9,
          length_includes_head=True, head_length=0.1, fc="b", ec="b", zorder=10)
plt.arrow(0, 0, u3[0], u3[1], head_width=0.1, linewidth=1, alpha=0.9,
          length_includes_head=True, head_length=0.1, fc="b", ec="b", zorder=10)
plt.text(u1[0] + 0.1, u1[1] - 0.05, r"$\mathbf{c_1}$", color="blue")
plt.text(u3[0] + 0.1, u3[1], r"$\mathbf{c_2}$", color="blue")
plt.xlabel("$x_1$")
plt.ylabel("$x_2$", rotation=0)
plt.axis([-1.4, 1.4, -1.4, 1.4])
plt.grid()

plt.subplot2grid((3, 2), (0, 1))
plt.plot([-2, 2], [0, 0], "k-", linewidth=2)
plt.plot(X_proj1[:, 0], np.zeros(m), "ro", alpha=0.3)
plt.gca().get_yaxis().set_ticks([])
plt.gca().get_xaxis().set_ticklabels([])
plt.axis([-2, 2, -1, 1])
plt.grid()

plt.subplot2grid((3, 2), (1, 1))
plt.plot([-2, 2], [0, 0], "k--", linewidth=2)
plt.plot(X_proj2[:, 0], np.zeros(m), "ro", alpha=0.3)
plt.gca().get_yaxis().set_ticks([])
plt.gca().get_xaxis().set_ticklabels([])
plt.axis([-2, 2, -1, 1])
plt.grid()

plt.subplot2grid((3, 2), (2, 1))
plt.plot([-2, 2], [0, 0], "k:", linewidth=2)
plt.plot(X_proj3[:, 0], np.zeros(m), "ro", alpha=0.3)
plt.gca().get_yaxis().set_ticks([])
plt.axis([-2, 2, -1, 1])
plt.xlabel("$z_1$")
plt.grid()
plt.show()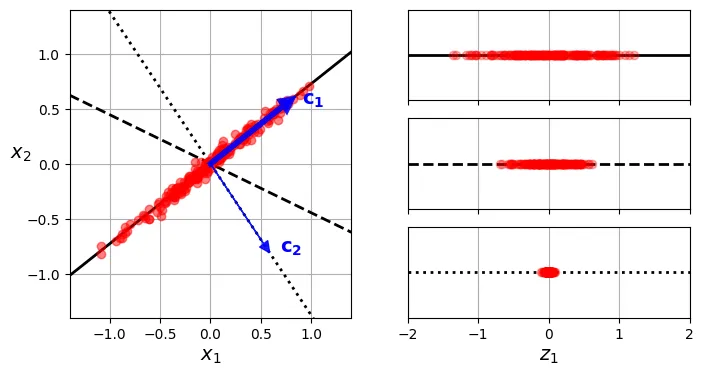

Thành phần chính (Principal Components)

PCA xác định trục chứa lượng phương sai lớn nhất trong tập huấn luyện gọi là thành phần chính thứ nhất. Thành phần chính thứ hai sẽ vuông góc với thành phần thứ nhất và chiếm lượng phương sai lớn thứ nhì, và cứ thế tiếp tục.

Trong Python, chúng ta có thể sử dụng kỹ thuật phân rã ma trận SVD (Singular Value Decomposition) để tìm các thành phần chính này. SVD sẽ phân rã ma trận dữ liệu huấn luyện $X$ thành tích của ba ma trận $U \Sigma V^T$, trong đó $V^T$ chứa các vector đơn vị định hướng các thành phần chính.

Dưới đây là cách thực hiện thủ công bằng NumPy:

import numpy as np
# X = [...]  # sử dụng tập dữ liệu 3D đã tạo ở phần trước

# Bước quan trọng: Luôn phải chuẩn hóa dữ liệu về trung bình 0 (centering)
X_centered = X - X.mean(axis=0)

# Sử dụng hàm svd của numpy để phân rã ma trận
U, s, Vt = np.linalg.svd(X_centered)

# Vt chứa các vector đơn vị của các thành phần chính
c1 = Vt[0] # Thành phần chính thứ nhất
c2 = Vt[1] # Thành phần chính thứ hai

Lưu ý: Theo lý thuyết toán học, SVD phân rã $X$ thành $U \Sigma V^T$. Tuy nhiên, hàm svd() của NumPy trả về U, s, và Vt (chính là $V^T$). s là một vector chứa các giá trị nằm trên đường chéo chính của ma trận $\Sigma$. Chúng ta có thể tái tạo lại ma trận $\Sigma$ từ s như sau:

# extra code – cách tạo lại ma trận Σ từ vector s
m, n = X.shape
Σ = np.zeros_like(X_centered)
Σ[:n, :n] = np.diag(s)

# Kiểm tra lại xem phép phân rã có chính xác không
assert np.allclose(X_centered, U @ Σ @ Vt)

Chiếu xuống d chiều (Projecting Down to d Dimensions)

Sau khi tìm được các thành phần chính, chúng ta có thể giảm chiều dữ liệu xuống $d$ chiều bằng cách nhân ma trận dữ liệu với $d$ thành phần chính đầu tiên (tương ứng với $d$ cột đầu tiên của ma trận $V^T$ chuyển vị).

W2 = Vt[:2].T # Lấy 2 thành phần chính đầu tiên
X2D = X_centered @ W2 # Chiếu dữ liệu xuống 2D

Sử dụng Scikit-Learn

Việc thực hiện thủ công như trên rất tốt cho mục đích học tập, nhưng trong thực tế, chúng ta nên dùng Scikit-Learn. Lớp PCA của Scikit-Learn tự động xử lý việc trừ trung bình (mean centering) và tính toán SVD.

from sklearn.decomposition import PCA

pca = PCA(n_components=2) # Khởi tạo PCA, yêu cầu giữ lại 2 chiều
X2D = pca.fit_transform(X) # Huấn luyện và biến đổi dữ liệu

Bạn có thể truy cập các thành phần chính (Principal Components) thông qua thuộc tính components_. Lưu ý rằng mỗi hàng là một thành phần chính.

pca.components_

array([[ 0.66824153,  0.73208333,  0.13231495],
       [ 0.74374636, -0.66151587, -0.09611511]])

Tỷ lệ phương sai giải thích (Explained Variance Ratio)

Một thông tin rất quan trọng là tỷ lệ phương sai giải thích. Nó cho biết tỷ lệ phương sai của tập dữ liệu nằm dọc theo trục của mỗi thành phần chính.

pca.explained_variance_ratio_

array([0.82279334, 0.10821224])

Kết quả trên cho thấy chiều thứ nhất giải thích khoảng 76% phương sai, trong khi chiều thứ hai giải thích khoảng 15%. Bằng cách chiếu xuống 2D, chúng ta đã mất đi khoảng 9% phương sai (thông tin).

1 - pca.explained_variance_ratio_.sum()  # Phần phương sai bị mất

np.float64(0.06899442237323172)

Chọn số chiều phù hợp

Thay vì chọn số chiều $d$ một cách tùy ý, thông thường chúng ta chọn $d$ sao cho tổng phương sai giải thích đạt một ngưỡng đủ lớn (ví dụ: 95%).

Dưới đây là ví dụ với bộ dữ liệu MNIST.

from sklearn.datasets import fetch_openml

# Tải dữ liệu MNIST
mnist = fetch_openml('mnist_784', as_frame=False)
X_train, y_train = mnist.data[:60_000], mnist.target[:60_000]
X_test, y_test = mnist.data[60_000:], mnist.target[60_000:]

# Chạy PCA mà chưa giảm chiều để tính toán phương sai
pca = PCA()
pca.fit(X_train)

# Tính tổng tích lũy của tỷ lệ phương sai
cumsum = np.cumsum(pca.explained_variance_ratio_)

# Tìm số chiều d để tổng phương sai đạt >= 0.95 (95%)
d = np.argmax(cumsum >= 0.95) + 1  # d = 154

d # Số chiều cần thiết

np.int64(154)

Thay vì tính toán thủ công như trên, Scikit-Learn cho phép bạn truyền trực tiếp một số thực trong khoảng (0.0, 1.0) vào tham số n_components. PCA sẽ tự động chọn số chiều nhỏ nhất để đạt được tỷ lệ phương sai đó.

pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(X_train)

pca.n_components_ # Số chiều thực tế được chọn

np.int64(154)

pca.explained_variance_ratio_.sum()  # Kiểm tra lại tổng phương sai

np.float64(0.9501960192613031)

Biểu đồ dưới đây (thường gọi là Scree Plot) hiển thị phương sai giải thích theo số chiều. Điểm “khuỷu tay” (elbow) thường là dấu hiệu tốt để chọn số chiều, nơi mà việc thêm chiều mới không còn mang lại nhiều thông tin đáng kể.

# extra code – ô này tạo ra Hình 7–8
plt.figure(figsize=(6, 4))
plt.plot(cumsum, linewidth=3)
plt.axis([0, 400, 0, 1])
plt.xlabel("Dimensions")
plt.ylabel("Explained Variance")
plt.plot([d, d], [0, 0.95], "k:")
plt.plot([0, d], [0.95, 0.95], "k:")
plt.plot(d, 0.95, "ko")
plt.annotate("Elbow", xy=(65, 0.85), xytext=(70, 0.7),
             arrowprops=dict(arrowstyle="->"))
plt.grid(True)
plt.show()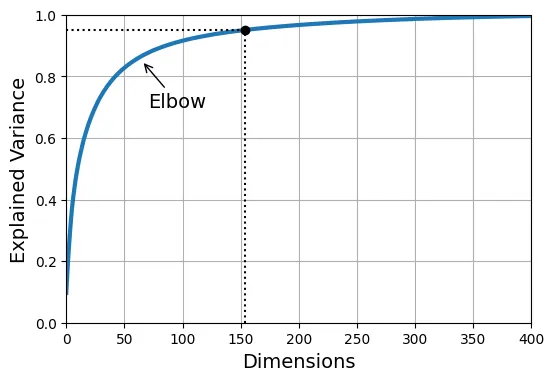

Chúng ta cũng có thể coi số chiều là một siêu tham số (hyperparameter) để tinh chỉnh trong quá trình huấn luyện mô hình. Ví dụ dưới đây sử dụng RandomizedSearchCV để tìm số chiều tối ưu cho PCA khi kết hợp với RandomForestClassifier.

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import RandomizedSearchCV
from sklearn.pipeline import make_pipeline

# Tạo một pipeline gồm PCA và Random Forest
clf = make_pipeline(PCA(random_state=42),
                    RandomForestClassifier(random_state=42))

# Định nghĩa không gian tham số để tìm kiếm
param_distrib = {
    "pca__n_components": np.arange(10, 80),
    "randomforestclassifier__n_estimators": np.arange(50, 500)}

# Tìm kiếm siêu tham số ngẫu nhiên
rnd_search = RandomizedSearchCV(clf, param_distrib, n_iter=10, cv=3,
                                random_state=42)
rnd_search.fit(X_train[:1000], y_train[:1000]) # Chỉ dùng 1000 mẫu để demo cho nhanh

RandomizedSearchCV(cv=3,
                   estimator=Pipeline(steps=[('pca', PCA(random_state=42)),
                                             ('randomforestclassifier',
                                              RandomForestClassifier(random_state=42))]),
                   param_distributions={'pca__n_components': array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26,
       27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43,
       44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60,
       6...
       414, 415, 416, 417, 418, 419, 420, 421, 422, 423, 424, 425, 426,
       427, 428, 429, 430, 431, 432, 433, 434, 435, 436, 437, 438, 439,
       440, 441, 442, 443, 444, 445, 446, 447, 448, 449, 450, 451, 452,
       453, 454, 455, 456, 457, 458, 459, 460, 461, 462, 463, 464, 465,
       466, 467, 468, 469, 470, 471, 472, 473, 474, 475, 476, 477, 478,
       479, 480, 481, 482, 483, 484, 485, 486, 487, 488, 489, 490, 491,
       492, 493, 494, 495, 496, 497, 498, 499])},
                   random_state=42)

RandomizedSearchCV(cv=3,
                   estimator=Pipeline(steps=[('pca', PCA(random_state=42)),
                                             ('randomforestclassifier',
                                              RandomForestClassifier(random_state=42))]),
                   param_distributions={'pca__n_components': array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26,
       27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43,
       44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60,
       6...
       414, 415, 416, 417, 418, 419, 420, 421, 422, 423, 424, 425, 426,
       427, 428, 429, 430, 431, 432, 433, 434, 435, 436, 437, 438, 439,
       440, 441, 442, 443, 444, 445, 446, 447, 448, 449, 450, 451, 452,
       453, 454, 455, 456, 457, 458, 459, 460, 461, 462, 463, 464, 465,
       466, 467, 468, 469, 470, 471, 472, 473, 474, 475, 476, 477, 478,
       479, 480, 481, 482, 483, 484, 485, 486, 487, 488, 489, 490, 491,
       492, 493, 494, 495, 496, 497, 498, 499])},
                   random_state=42)

Pipeline(steps=[('pca', PCA(n_components=np.int64(57), random_state=42)),
                ('randomforestclassifier',
                 RandomForestClassifier(n_estimators=np.int64(475),
                                        random_state=42))])

PCA(n_components=np.int64(57), random_state=42)

RandomForestClassifier(n_estimators=np.int64(475), random_state=42)

print(rnd_search.best_params_) # In ra tham số tốt nhất tìm được

{'randomforestclassifier__n_estimators': np.int64(475), 'pca__n_components': np.int64(57)}

Tương tự, chúng ta có thể thử với mô hình tuyến tính như SGDClassifier.

from sklearn.linear_model import SGDClassifier
from sklearn.model_selection import GridSearchCV

clf = make_pipeline(PCA(random_state=42), SGDClassifier())
param_grid = {"pca__n_components": np.arange(10, 80)}
grid_search = GridSearchCV(clf, param_grid, cv=3)
grid_search.fit(X_train[:1000], y_train[:1000])

GridSearchCV(cv=3,
             estimator=Pipeline(steps=[('pca', PCA(random_state=42)),
                                       ('sgdclassifier', SGDClassifier())]),
             param_grid={'pca__n_components': array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26,
       27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43,
       44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60,
       61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77,
       78, 79])})

GridSearchCV(cv=3,
             estimator=Pipeline(steps=[('pca', PCA(random_state=42)),
                                       ('sgdclassifier', SGDClassifier())]),
             param_grid={'pca__n_components': array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26,
       27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43,
       44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60,
       61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77,
       78, 79])})

Pipeline(steps=[('pca', PCA(n_components=np.int64(78), random_state=42)),
                ('sgdclassifier', SGDClassifier())])

PCA(n_components=np.int64(78), random_state=42)

SGDClassifier()

grid_search.best_params_

{'pca__n_components': np.int64(78)}

PCA dùng để nén dữ liệu (Compression)

Sau khi giảm chiều dữ liệu (nén), chúng ta có thể dùng phép biến đổi ngược để tái tạo lại dữ liệu gốc. Dĩ nhiên, do đã mất một phần thông tin (5% phương sai), dữ liệu tái tạo sẽ không hoàn toàn giống hệt dữ liệu ban đầu, nhưng thường sẽ rất gần.

pca = PCA(0.95)
X_reduced = pca.fit_transform(X_train, y_train) # Nén
X_recovered = pca.inverse_transform(X_reduced)  # Giải nén

Đoạn mã dưới đây so sánh hình ảnh gốc và hình ảnh sau khi nén rồi giải nén. Bạn có thể thấy chất lượng giảm đi đôi chút nhưng nội dung chính vẫn được bảo toàn.

# extra code – ô này tạo ra Hình 7–9
plt.figure(figsize=(7, 4))
for idx, X in enumerate((X_train[::2100], X_recovered[::2100])):
    plt.subplot(1, 2, idx + 1)
    plt.title(["Original", "Compressed"][idx])
    for row in range(5):
        for col in range(5):
            plt.imshow(X[row * 5 + col].reshape(28, 28), cmap="binary",
                       vmin=0, vmax=255, extent=(row, row + 1, col, col + 1))
            plt.axis([0, 5, 0, 5])
            plt.axis("off")

Randomized PCA

Nếu bạn thiết lập svd_solver="randomized", Scikit-Learn sẽ sử dụng thuật toán ngẫu nhiên để tìm xấp xỉ các thành phần chính đầu tiên. Phương pháp này nhanh hơn nhiều so với PCA thông thường khi số chiều $d$ nhỏ hơn nhiều so với số lượng đặc trưng $n$.

rnd_pca = PCA(n_components=154, svd_solver="randomized", random_state=42)
X_reduced = rnd_pca.fit_transform(X_train)

Incremental PCA (IPCA)

Khi tập dữ liệu quá lớn để chứa vừa trong bộ nhớ (RAM), bạn có thể sử dụng Incremental PCA. Nó cho phép chia dữ liệu thành các lô nhỏ (mini-batches) và đưa từng lô vào thuật toán.

from sklearn.decomposition import IncrementalPCA

n_batches = 100
inc_pca = IncrementalPCA(n_components=154)

# Chia dữ liệu thành các phần nhỏ và huấn luyện từng phần
for X_batch in np.array_split(X_train, n_batches):
    inc_pca.partial_fit(X_batch)

X_reduced = inc_pca.transform(X_train)

Một cách khác để xử lý dữ liệu lớn là sử dụng lớp memmap của NumPy. memmap cho phép thao tác với một mảng lớn lưu trên đĩa cứng như thể nó đang nằm trong RAM.

# Tạo file memmap và ghi dữ liệu vào đĩa
filename = "my_mnist.mmap"
X_mmap = np.memmap(filename, dtype='float32', mode='write', shape=X_train.shape)
X_mmap[:] = X_train  # Ghi dữ liệu (có thể dùng vòng lặp để ghi từng phần)
X_mmap.flush() # Đảm bảo dữ liệu đã được lưu xuống đĩa

Sau đó, chúng ta có thể tải dữ liệu lên (ở chế độ chỉ đọc readonly) và sử dụng nó để huấn luyện IncrementalPCA. batch_size sẽ giúp IPCA tự động quản lý việc tải từng phần dữ liệu.

X_mmap = np.memmap(filename, dtype="float32", mode="readonly").reshape(-1, 784)

batch_size = X_mmap.shape[0] // n_batches
inc_pca = IncrementalPCA(n_components=154, batch_size=batch_size)
inc_pca.fit(X_mmap)

IncrementalPCA(batch_size=600, n_components=154)

IncrementalPCA(batch_size=600, n_components=154)

Phép chiếu ngẫu nhiên (Random Projection)

Theo bổ đề Johnson-Lindenstrauss, nếu bạn chiếu các điểm dữ liệu từ không gian nhiều chiều xuống không gian ít chiều hơn (nhưng đủ lớn) bằng một ma trận ngẫu nhiên, khoảng cách giữa các điểm sẽ được bảo toàn xấp xỉ. Phương pháp này rất mạnh mẽ và cực kỳ nhanh vì không cần huấn luyện (không cần học các tham số từ dữ liệu).

Đầu tiên, hãy tính số chiều tối thiểu cần thiết để đảm bảo sai số (epsilon $\varepsilon$) nằm trong giới hạn cho phép.

# Cảnh báo: phần này có thể tiêu tốn gần 2.5 GB RAM.
from sklearn.random_projection import johnson_lindenstrauss_min_dim

m, ε = 5_000, 0.1
d = johnson_lindenstrauss_min_dim(m, eps=ε)
d

np.int64(7300)

# extra code – hiển thị công thức tính toán johnson_lindenstrauss_min_dim
d = int(4 * np.log(m) / (ε ** 2 / 2 - ε ** 3 / 3))
d

7300

Bây giờ chúng ta sẽ tạo một ma trận ngẫu nhiên $P$ và dùng nó để chiếu dữ liệu.

n = 20_000
rng = np.random.default_rng(seed=42)
P = rng.standard_normal((d, n)) / np.sqrt(d)  # Độ lệch chuẩn = căn bậc 2 của phương sai
X = rng.standard_normal((m, n))  # Tạo dữ liệu giả lập
X_reduced = X @ P.T

Scikit-Learn cung cấp lớp GaussianRandomProjection để thực hiện việc này dễ dàng hơn.

from sklearn.random_projection import GaussianRandomProjection

gaussian_rnd_proj = GaussianRandomProjection(eps=ε, random_state=42)
X_reduced = gaussian_rnd_proj.fit_transform(X)  # Kết quả tương tự như trên

Bạn cũng có thể thử khôi phục lại dữ liệu bằng cách tính ma trận giả nghịch đảo (pseudo-inverse), nhưng lưu ý là quá trình này có thể tốn nhiều thời gian tính toán.

# Cảnh báo: ô này có thể mất vài phút để chạy
components_pinv = np.linalg.pinv(gaussian_rnd_proj.components_)
X_recovered = X_reduced @ components_pinv.T

Nếu dữ liệu của bạn thưa (sparse matrix), hãy sử dụng SparseRandomProjection. Nó nhanh hơn và tiết kiệm bộ nhớ hơn.

# extra code – so sánh hiệu năng giữa Gaussian và Sparse RP
from sklearn.random_projection import SparseRandomProjection

print("GaussianRandomProjection fit")
%timeit GaussianRandomProjection(random_state=42).fit(X)

print("SparseRandomProjection fit")
%timeit SparseRandomProjection(random_state=42).fit(X)

gaussian_rnd_proj = GaussianRandomProjection(random_state=42).fit(X)
sparse_rnd_proj = SparseRandomProjection(random_state=42).fit(X)

print("GaussianRandomProjection transform")
%timeit gaussian_rnd_proj.transform(X)

print("SparseRandomProjection transform")
%timeit sparse_rnd_proj.transform(X)

GaussianRandomProjection fit
5.22 s ± 442 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
SparseRandomProjection fit
3.84 s ± 799 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
GaussianRandomProjection transform
50.3 s ± 699 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
SparseRandomProjection transform
7.12 s ± 1.28 s per loop (mean ± std. dev. of 7 runs, 1 loop each)

LLE (Locally Linear Embedding)

Nhúng tuyến tính cục bộ (Locally Linear Embedding - LLE) là một kỹ thuật Học đa tạp phi tuyến tính (nonlinear manifold learning). Thay vì dựa vào phép chiếu, LLE hoạt động bằng cách đo lường mối quan hệ tuyến tính của mỗi điểm dữ liệu với các láng giềng gần nhất (nearest neighbors) của nó, sau đó tìm kiếm một biểu diễn cấp thấp sao cho các mối quan hệ cục bộ này được bảo toàn tốt nhất.

from sklearn.datasets import make_swiss_roll
from sklearn.manifold import LocallyLinearEmbedding

X_swiss, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=42)
lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10, random_state=42)
X_unrolled = lle.fit_transform(X_swiss)

Kết quả bên dưới cho thấy LLE đã trải phẳng Swiss roll ra rất tốt, bảo toàn khoảng cách giữa các điểm gần nhau. Tuy nhiên, khoảng cách giữa các điểm xa nhau có thể không được bảo toàn tốt.

# extra code – ô này tạo ra Hình 7–10
plt.scatter(X_unrolled[:, 0], X_unrolled[:, 1],
            c=t, cmap=darker_hot)
plt.xlabel("$z_1$")
plt.ylabel("$z_2$", rotation=0)
plt.axis([-0.06, 0.055, -0.085, 0.075])
plt.grid(True)
plt.title("Unrolled swiss roll using LLE")
plt.show()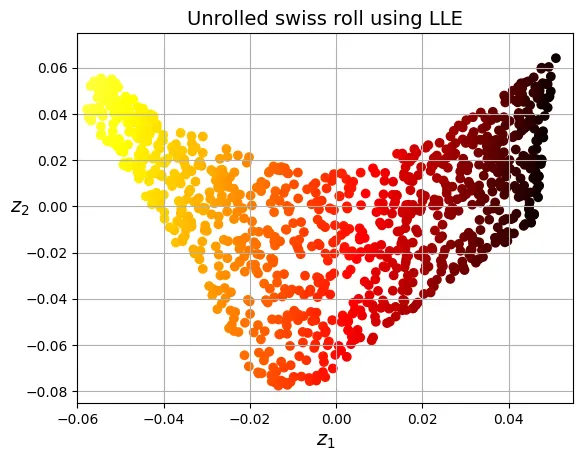

Biểu đồ dưới đây xác nhận rằng LLE hoạt động tốt vì tọa độ mới $z_1$ có mối tương quan chặt chẽ với màu sắc $t$ (vị trí gốc trên cuộn).

# extra code – hiển thị tương quan giữa z1 và t
plt.title("$z_1$ vs $t$")
plt.scatter(X_unrolled[:, 0], t, c=t, cmap=darker_hot)
plt.xlabel("$z_1$")
plt.ylabel("$t$", rotation=0)
plt.grid(True)
plt.show()

Các kỹ thuật giảm chiều khác

Ngoài LLE, còn có nhiều kỹ thuật giảm chiều phổ biến khác:

• MDS (Multidimensional Scaling): Cố gắng bảo toàn khoảng cách giữa các điểm dữ liệu.
• Isomap: Bảo toàn khoảng cách trắc địa (geodesic distance) giữa các điểm.
• t-SNE (t-Distributed Stochastic Neighbor Embedding): Rất mạnh mẽ trong việc trực quan hóa các cụm dữ liệu, đặc biệt là dữ liệu hình ảnh.

# MDS
from sklearn.manifold import MDS
mds = MDS(n_components=2, normalized_stress=False, random_state=42)
X_reduced_mds = mds.fit_transform(X_swiss)

# Isomap
from sklearn.manifold import Isomap
isomap = Isomap(n_components=2)
X_reduced_isomap = isomap.fit_transform(X_swiss)

# t-SNE
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, init="random", learning_rate="auto",
            random_state=42)
X_reduced_tsne = tsne.fit_transform(X_swiss)

Hãy cùng so sánh kết quả trực quan hóa của ba phương pháp này:

# extra code – ô này tạo ra Hình 7–11
titles = ["MDS", "Isomap", "t-SNE"]
plt.figure(figsize=(11, 4))

for subplot, title, X_reduced in zip((131, 132, 133), titles,
                                     (X_reduced_mds, X_reduced_isomap, X_reduced_tsne)):
    plt.subplot(subplot)
    plt.title(title)
    plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=t, cmap=darker_hot)
    plt.xlabel("$z_1$")
    if subplot == 131:
        plt.ylabel("$z_2$", rotation=0)
    plt.grid(True)

plt.show()

Phần mở rộng – Kernel PCA

Tương tự như trong SVM (Support Vector Machines), chúng ta có thể áp dụng thủ thuật hạt nhân (Kernel trick) vào PCA để thực hiện các phép chiếu phi tuyến tính phức tạp. Kỹ thuật này được gọi là Kernel PCA (kPCA).

from sklearn.decomposition import KernelPCA

rbf_pca = KernelPCA(n_components=2, kernel="rbf", gamma=0.04, random_state=42)
X_reduced = rbf_pca.fit_transform(X_swiss)

Dưới đây là so sánh kết quả của kPCA với các loại hạt nhân khác nhau: Tuyến tính (Linear), RBF và Sigmoid.

lin_pca = KernelPCA(kernel="linear")
rbf_pca = KernelPCA(kernel="rbf", gamma=0.002)
sig_pca = KernelPCA(kernel="sigmoid", gamma=0.002, coef0=1)

kernel_pcas = ((lin_pca, "Linear kernel"),
               (rbf_pca, rf"RBF kernel, $\gamma={rbf_pca.gamma}$"),
               (sig_pca, rf"Sigmoid kernel, $\gamma={sig_pca.gamma}, r={sig_pca.coef0}$"))

plt.figure(figsize=(11, 3.5))
for idx, (kpca, title) in enumerate(kernel_pcas):
    kpca.n_components = 2
    kpca.random_state = 42
    X_reduced = kpca.fit_transform(X_swiss)

    plt.subplot(1, 3, idx + 1)
    plt.title(title)
    plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=t, cmap=darker_hot)
    plt.xlabel("$z_1$")
    if idx == 0:
        plt.ylabel("$z_2$", rotation=0)
    plt.grid()

plt.show()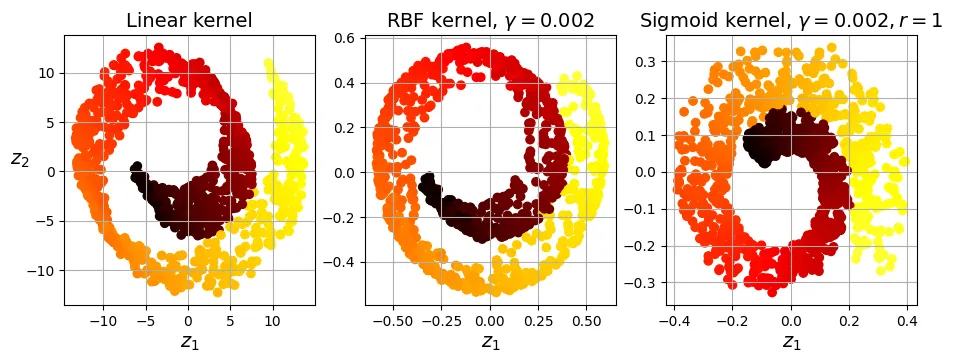

Ôn tập

1. Động lực chính của giảm chiều dữ liệu:

   • Tăng tốc độ thuật toán huấn luyện (đôi khi còn giúp loại bỏ nhiễu và đặc trưng thừa, cải thiện hiệu suất).
   • Trực quan hóa dữ liệu để tìm kiếm pattern.
   • Tiết kiệm không gian lưu trữ (nén dữ liệu).

2. Nhược điểm:

   • Mất thông tin, có thể làm giảm hiệu suất mô hình.
   • Tốn chi phí tính toán.
   • Tăng độ phức tạp cho pipeline.
   • Các đặc trưng mới thường khó diễn giải.

3. Lời nguyền của số chiều (Curse of Dimensionality):

   • Trong không gian nhiều chiều, các điểm dữ liệu thường nằm rất xa nhau (thưa thớt). Điều này làm tăng nguy cơ overfitting và khiến việc tìm kiếm mẫu trở nên khó khăn nếu không có lượng dữ liệu khổng lồ.

4. Khả năng đảo ngược:

   • Thường là không thể đảo ngược hoàn hảo vì thông tin đã bị mất. PCA có thể đảo ngược tương đối tốt (có sai số), nhưng t-SNE thì không có hàm đảo ngược đơn giản.

5. PCA và dữ liệu phi tuyến:

   • PCA có thể loại bỏ các chiều vô dụng, nhưng nếu dữ liệu bị uốn cong (như Swiss roll) và không có chiều dư thừa tuyến tính, PCA sẽ làm mất quá nhiều thông tin (nó đè bẹp cuộn bánh thay vì mở nó ra).

6. Số chiều cần thiết cho 95% phương sai:

   • Phụ thuộc hoàn toàn vào dữ liệu. Nếu dữ liệu thẳng hàng, chỉ cần 1 chiều. Nếu dữ liệu ngẫu nhiên hoàn toàn (nhiễu trắng) trong 1000 chiều, ta cần gần 950 chiều.

7. Lựa chọn thuật toán PCA:

   • Regular PCA: Mặc định, tốt nếu dữ liệu vừa RAM.
   • Incremental PCA: Dữ liệu quá lớn (không vừa RAM) hoặc cần học online.
   • Randomized PCA: Cần tốc độ cao, dữ liệu vừa RAM, muốn giảm chiều mạnh.
   • Random Projection: Dữ liệu cực kỳ nhiều chiều và thưa.

8. Đánh giá thuật toán giảm chiều:

   • Đo sai số tái tạo (nếu có thể đảo ngược).
   • Đo hiệu suất của thuật toán học máy phía sau (ví dụ: độ chính xác của bộ phân lớp).
   • Có thể nối chuỗi (chaining): Dùng PCA giảm bớt chiều rác trước, sau đó dùng LLE (chậm hơn) để học đa tạp.

Thực hành 1: Bài tập thực hành với MNIST

Bài tập: Tải bộ dữ liệu MNIST và chia thành tập huấn luyện (60,000 mẫu đầu) và tập kiểm tra (10,000 mẫu còn lại).

# Dữ liệu MNIST đã được tải ở phần trước
X_train = mnist.data[:60000]
y_train = mnist.target[:60000]
X_test = mnist.data[60000:]
y_test = mnist.target[60000:]

Bài tập: Huấn luyện một bộ phân loại Random Forest trên tập dữ liệu gốc, đo thời gian và đánh giá độ chính xác.

from sklearn.ensemble import RandomForestClassifier

rnd_clf = RandomForestClassifier(n_estimators=100, random_state=42)

# Đo thời gian huấn luyện
%time rnd_clf.fit(X_train, y_train)

CPU times: user 1min, sys: 83.1 ms, total: 1min
Wall time: 1min 1s

RandomForestClassifier(random_state=42)

RandomForestClassifier(random_state=42)

from sklearn.metrics import accuracy_score

y_pred = rnd_clf.predict(X_test)
accuracy_score(y_test, y_pred)

0.9705

Bài tập: Tiếp theo, sử dụng PCA để giảm chiều dữ liệu với tỷ lệ phương sai giải thích là 95%.

from sklearn.decomposition import PCA

pca = PCA(n_components=0.95)
X_train_reduced = pca.fit_transform(X_train)

Bài tập: Huấn luyện lại Random Forest trên dữ liệu đã giảm chiều và so sánh thời gian.

rnd_clf_with_pca = RandomForestClassifier(n_estimators=100, random_state=42)
%time rnd_clf_with_pca.fit(X_train_reduced, y_train)

CPU times: user 3min 14s, sys: 261 ms, total: 3min 14s
Wall time: 3min 17s

RandomForestClassifier(random_state=42)

RandomForestClassifier(random_state=42)

Kết quả bất ngờ: Thời gian huấn luyện thực tế lại chậm hơn gấp 3 lần! Tại sao lại như vậy?

Lý do là PCA xoay dữ liệu để tối ưu hóa phương sai, nhưng điều này làm mất tính trực giao của các đặc trưng gốc (pixel). Random Forest hoạt động bằng cách tìm các ngưỡng cắt vuông góc với trục tọa độ. Khi dữ liệu bị xoay nghiêng, cây quyết định phải vất vả hơn nhiều để tìm ra đường chia cắt bậc thang để xấp xỉ đường chéo. Vì vậy, PCA không phải lúc nào cũng giúp tăng tốc độ cho mọi thuật toán.

Hãy kiểm tra độ chính xác:

X_test_reduced = pca.transform(X_test)
y_pred = rnd_clf_with_pca.predict(X_test_reduced)
accuracy_score(y_test, y_pred)

0.9488

Độ chính xác cũng giảm đi đáng kể. Trong trường hợp này, PCA vừa làm chậm quá trình huấn luyện vừa làm giảm hiệu suất.

Bài tập: Thử lại với SGDClassifier. Liệu PCA có giúp ích gì không?

from sklearn.linear_model import SGDClassifier

sgd_clf = SGDClassifier(random_state=42)
%time sgd_clf.fit(X_train, y_train)

CPU times: user 3min 21s, sys: 291 ms, total: 3min 22s
Wall time: 3min 24s

SGDClassifier(random_state=42)

SGDClassifier(random_state=42)

y_pred = sgd_clf.predict(X_test)
accuracy_score(y_test, y_pred)

0.874

SGDClassifier huấn luyện khá lâu trên tập dữ liệu gốc. Bây giờ hãy thử trên tập dữ liệu đã giảm chiều:

sgd_clf_with_pca = SGDClassifier(random_state=42)
%time sgd_clf_with_pca.fit(X_train_reduced, y_train)

CPU times: user 49.8 s, sys: 41.1 ms, total: 49.8 s
Wall time: 50.2 s

SGDClassifier(random_state=42)

SGDClassifier(random_state=42)

y_pred = sgd_clf_with_pca.predict(X_test_reduced)
accuracy_score(y_test, y_pred)

0.8959

Tuyệt vời! Với SGD, PCA đã giúp tăng tốc độ lên khoảng 6 lần và thậm chí còn cải thiện độ chính xác một chút. Điều này chứng tỏ hiệu quả của PCA phụ thuộc rất nhiều vào loại mô hình và dữ liệu bạn đang sử dụng.

Thực hành 2: Bài tập trực quan hóa với t-SNE

Bài tập: Sử dụng t-SNE để giảm 5,000 hình ảnh đầu tiên của tập MNIST xuống 2 chiều và vẽ biểu đồ phân tán (scatterplot).

X_sample, y_sample = X_train[:5000], y_train[:5000]

from sklearn.manifold import TSNE

tsne = TSNE(n_components=2, init="random", learning_rate="auto",
            random_state=42)
%time X_reduced = tsne.fit_transform(X_sample)

CPU times: user 1min 5s, sys: 158 ms, total: 1min 5s
Wall time: 1min 6s

Bây giờ chúng ta sẽ vẽ biểu đồ, sử dụng màu sắc khác nhau cho mỗi chữ số.

plt.figure(figsize=(13, 10))
plt.scatter(X_reduced[:, 0], X_reduced[:, 1],
            c=y_sample.astype(np.int8), cmap="jet", alpha=0.5)
plt.axis('off')
plt.colorbar()
plt.show()

Biểu đồ t-SNE cho thấy các cụm chữ số được tách biệt khá tốt. Tuy nhiên, vẫn có sự chồng chéo, ví dụ như giữa số 4 và số 9. Hãy thử tập trung vào hai số này:

plt.figure(figsize=(9, 9))
cmap = plt.cm.jet
for digit in ('4', '9'):
    plt.scatter(X_reduced[y_sample == digit, 0], X_reduced[y_sample == digit, 1],
                c=[cmap(float(digit) / 9)], alpha=0.5)
plt.axis('off')
plt.show()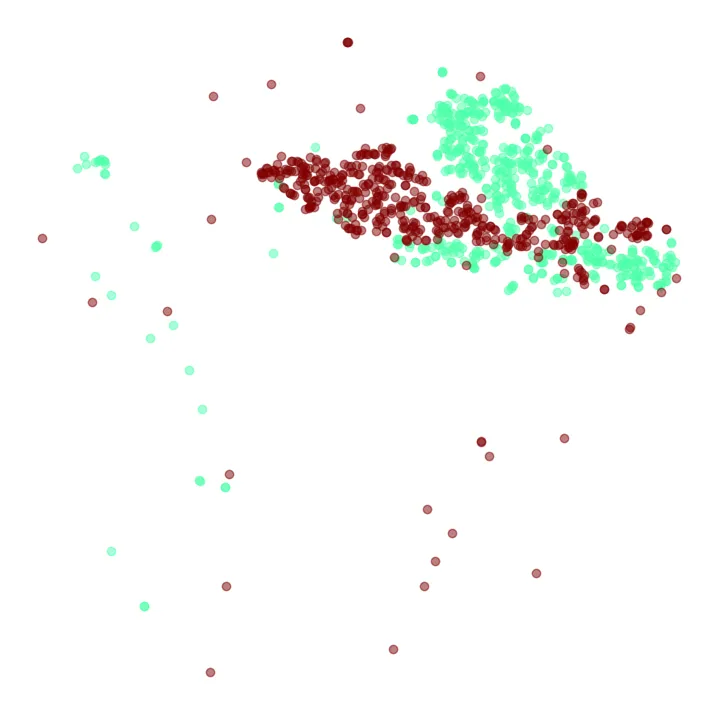

Chúng ta có thể thử chạy t-SNE lại chỉ với tập con chứa số 4 và 9 để xem kết quả có tốt hơn không.

idx = (y_sample == '4') | (y_sample == '9')
X_subset = X_sample[idx]
y_subset = y_sample[idx]

tsne_subset = TSNE(n_components=2, init="random", learning_rate="auto",
                   random_state=42)
X_subset_reduced = tsne_subset.fit_transform(X_subset)

plt.figure(figsize=(9, 9))
for digit in ('4', '9'):
    plt.scatter(X_subset_reduced[y_subset == digit, 0],
                X_subset_reduced[y_subset == digit, 1],
                c=[cmap(float(digit) / 9)], alpha=0.5)
plt.axis('off')
plt.show()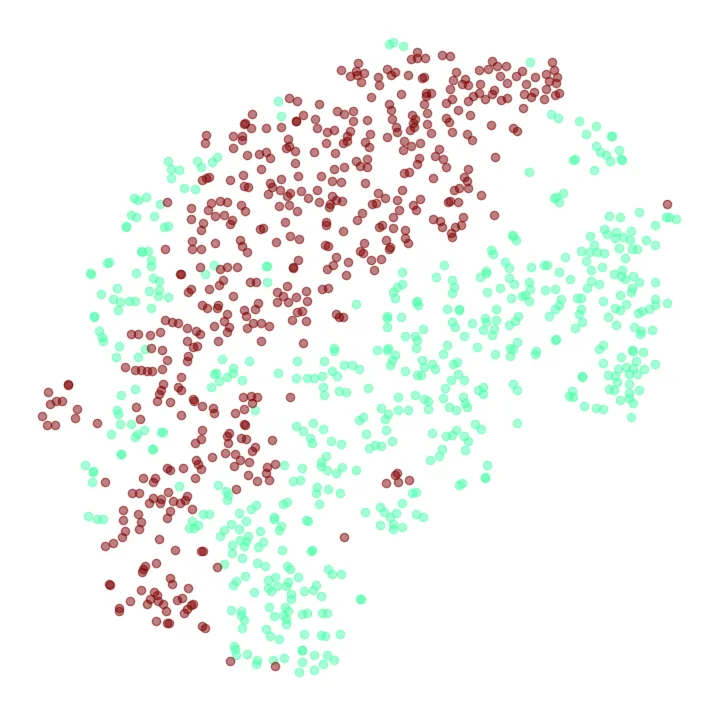

Bài tập nâng cao: Hãy tạo một biểu đồ đẹp hơn bằng cách thay thế các điểm chấm bằng chính hình ảnh của các con số.

Hàm plot_digits dưới đây sẽ thực hiện điều đó. Nó sử dụng MinMaxScaler để chuẩn hóa tọa độ và đảm bảo các hình ảnh không đè lên nhau quá nhiều (dùng min_distance).

from sklearn.preprocessing import MinMaxScaler
from matplotlib.offsetbox import AnnotationBbox, OffsetImage

def plot_digits(X, y, min_distance=0.04, images=None, figsize=(13, 10)):
    # Chuẩn hóa đặc trưng về khoảng [0, 1]
    X_normalized = MinMaxScaler().fit_transform(X)

    # Danh sách tọa độ các hình đã vẽ (khởi tạo điểm giả để tránh lỗi logic)
    neighbors = np.array([[10., 10.]])

    plt.figure(figsize=figsize)
    cmap = plt.cm.jet
    digits = np.unique(y)

    # Vẽ các chấm màu trước
    for digit in digits:
        plt.scatter(X_normalized[y == digit, 0], X_normalized[y == digit, 1],
                    c=[cmap(float(digit) / 9)], alpha=0.5)
    plt.axis("off")
    ax = plt.gca()

    # Vẽ hình ảnh số
    for index, image_coord in enumerate(X_normalized):
        closest_distance = np.linalg.norm(neighbors - image_coord, axis=1).min()
        if closest_distance > min_distance:
            neighbors = np.r_[neighbors, [image_coord]]
            if images is None:
                plt.text(image_coord[0], image_coord[1], str(int(y[index])),
                         color=cmap(float(y[index]) / 9),
                         fontdict={"weight": "bold", "size": 16})
            else:
                image = images[index].reshape(28, 28)
                imagebox = AnnotationBbox(OffsetImage(image, cmap="binary"),
                                          image_coord)
                ax.add_artist(imagebox)

Thử nghiệm hàm plot_digits với dữ liệu t-SNE:

plot_digits(X_reduced, y_sample)

Và bây giờ là phiên bản đầy đủ với hình ảnh các chữ số:

plot_digits(X_reduced, y_sample, images=X_sample, figsize=(35, 25))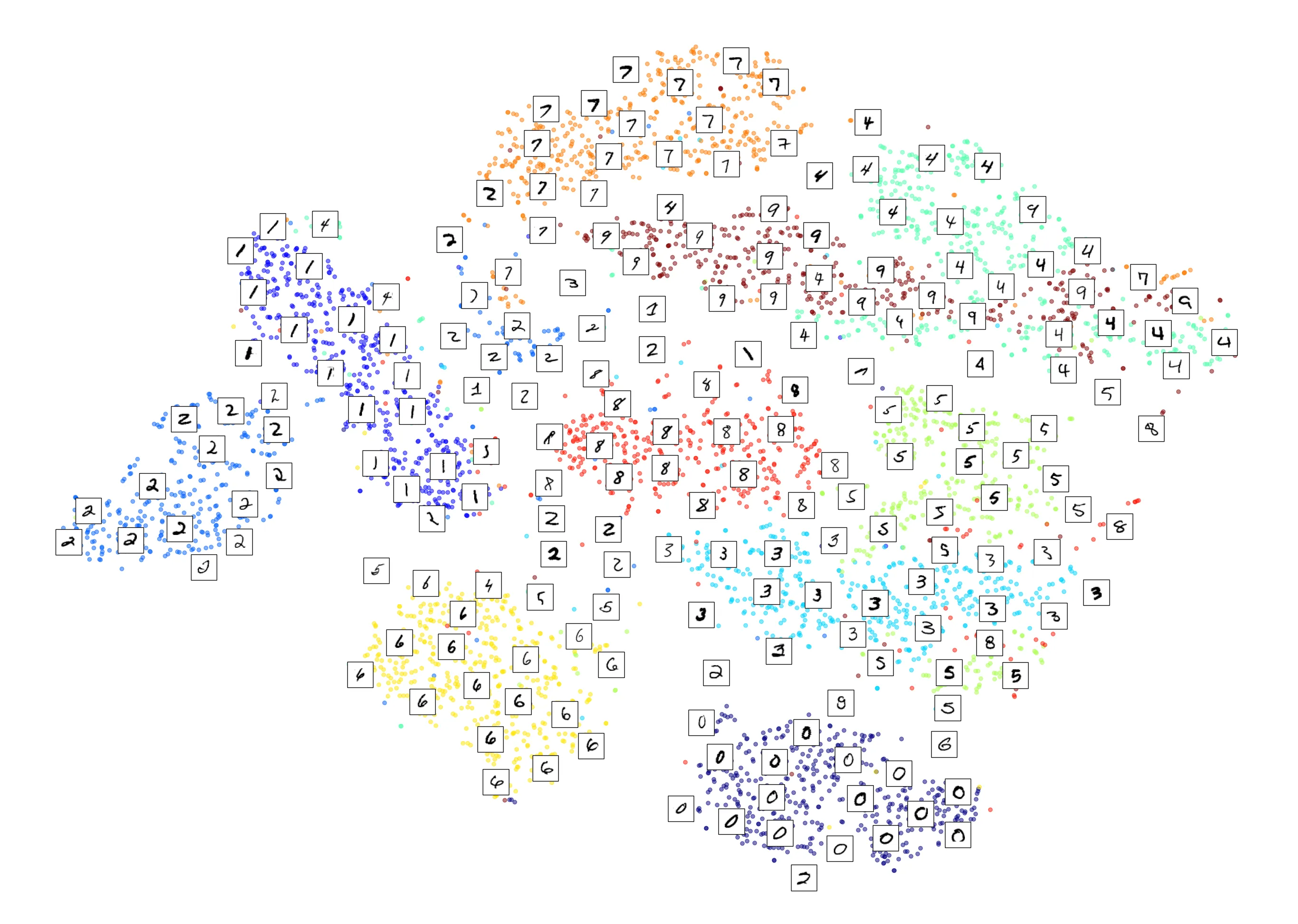

Hãy thử áp dụng kỹ thuật này cho tập con số 4 và 9:

plot_digits(X_subset_reduced, y_subset, images=X_subset, figsize=(22, 22))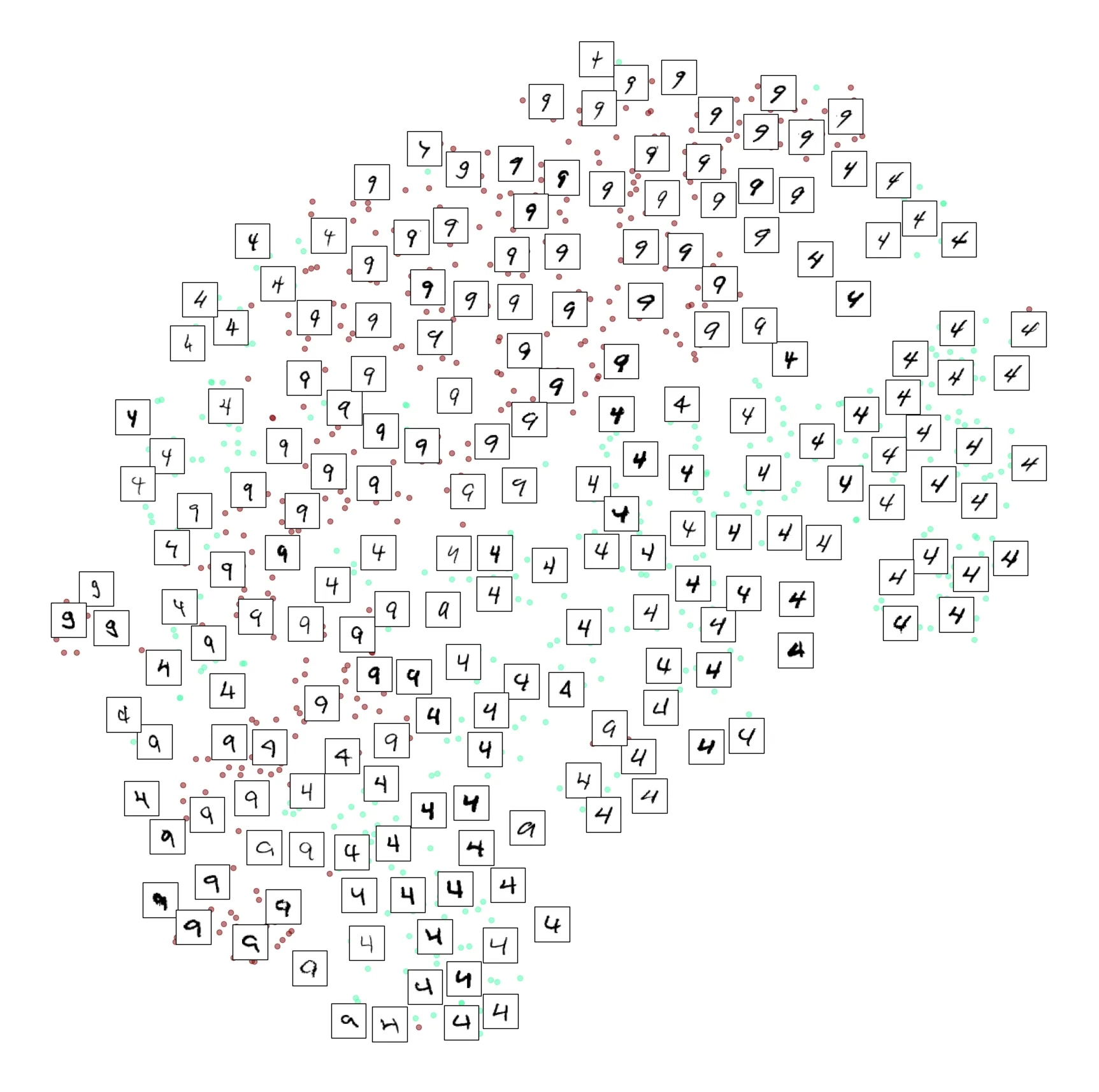

Bài tập: Thử nghiệm với các thuật toán khác như PCA, LLE, MDS và so sánh.

# PCA: Rất nhanh nhưng chồng chéo nhiều
pca = PCA(n_components=2, random_state=42)
%time X_pca_reduced = pca.fit_transform(X_sample)
plot_digits(X_pca_reduced, y_sample)
plt.show()

CPU times: user 446 ms, sys: 47.3 ms, total: 493 ms
Wall time: 288 ms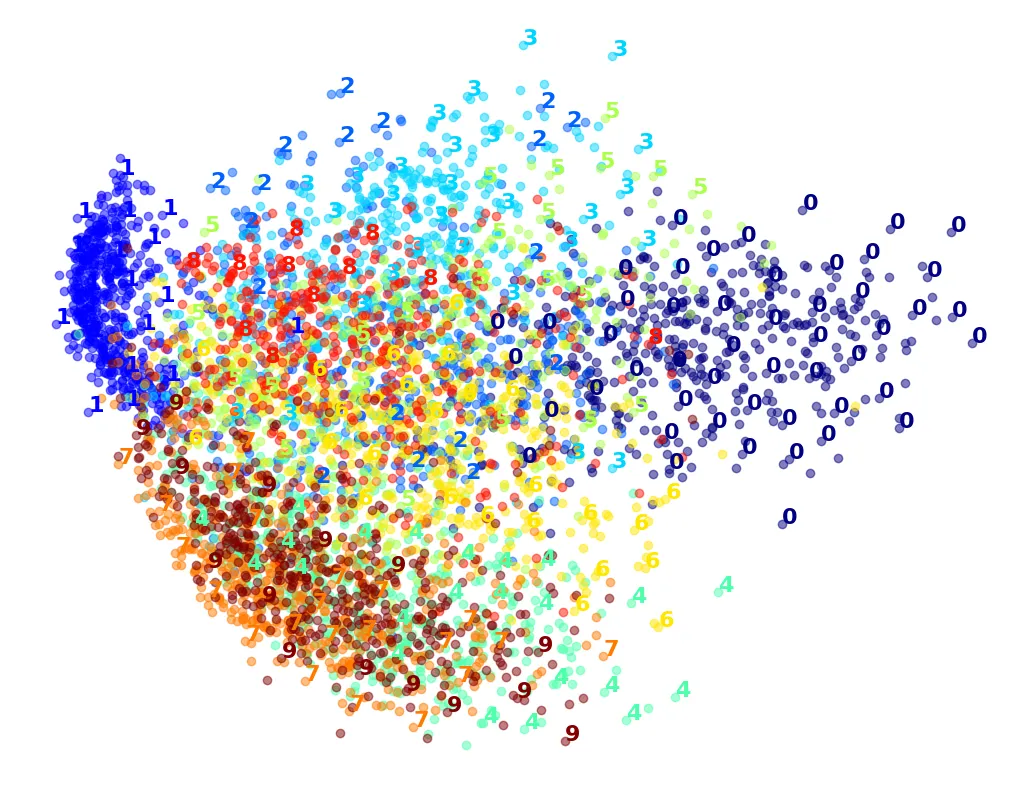

# LLE: Chậm hơn PCA, kết quả cũng chưa thực sự tốt
lle = LocallyLinearEmbedding(n_components=2, random_state=42)
%time X_lle_reduced = lle.fit_transform(X_sample)
plot_digits(X_lle_reduced, y_sample)
plt.show()

CPU times: user 4.68 s, sys: 81.4 ms, total: 4.76 s
Wall time: 4.85 s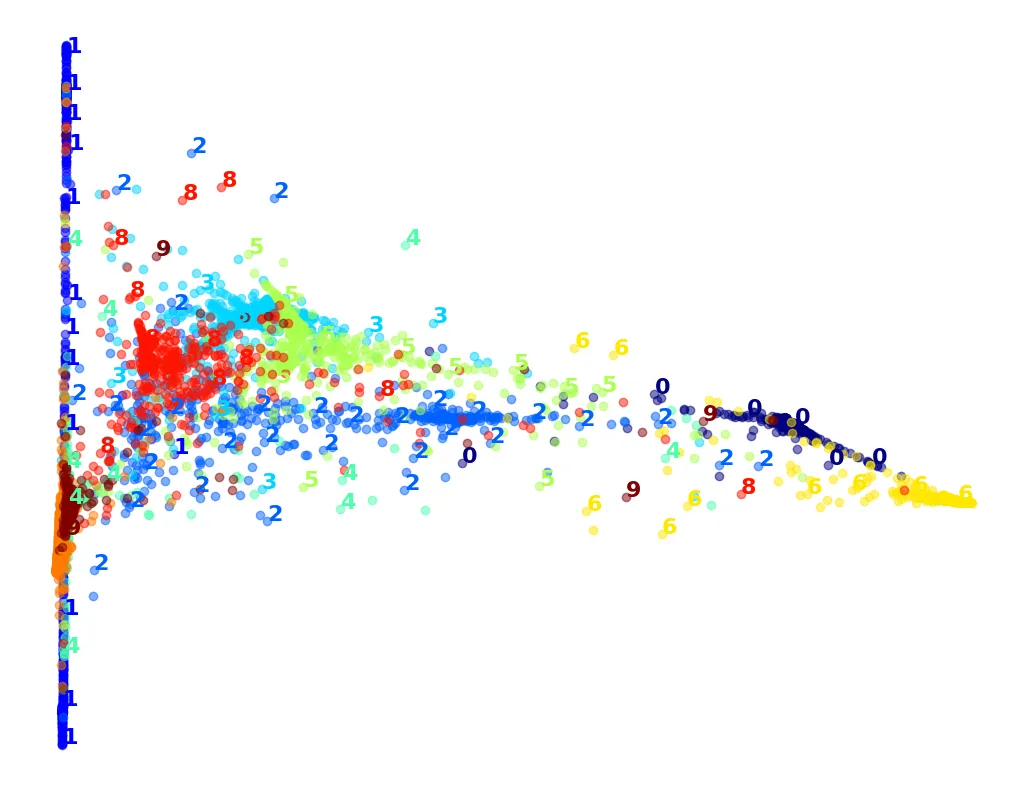

# Kết hợp PCA + LLE: Nhanh hơn LLE gốc một chút nhưng kết quả tương tự
pca_lle = make_pipeline(PCA(n_components=0.95),
                        LocallyLinearEmbedding(n_components=2, random_state=42))
%time X_pca_lle_reduced = pca_lle.fit_transform(X_sample)
plot_digits(X_pca_lle_reduced, y_sample)
plt.show()

CPU times: user 4.78 s, sys: 36.9 ms, total: 4.82 s
Wall time: 3.57 s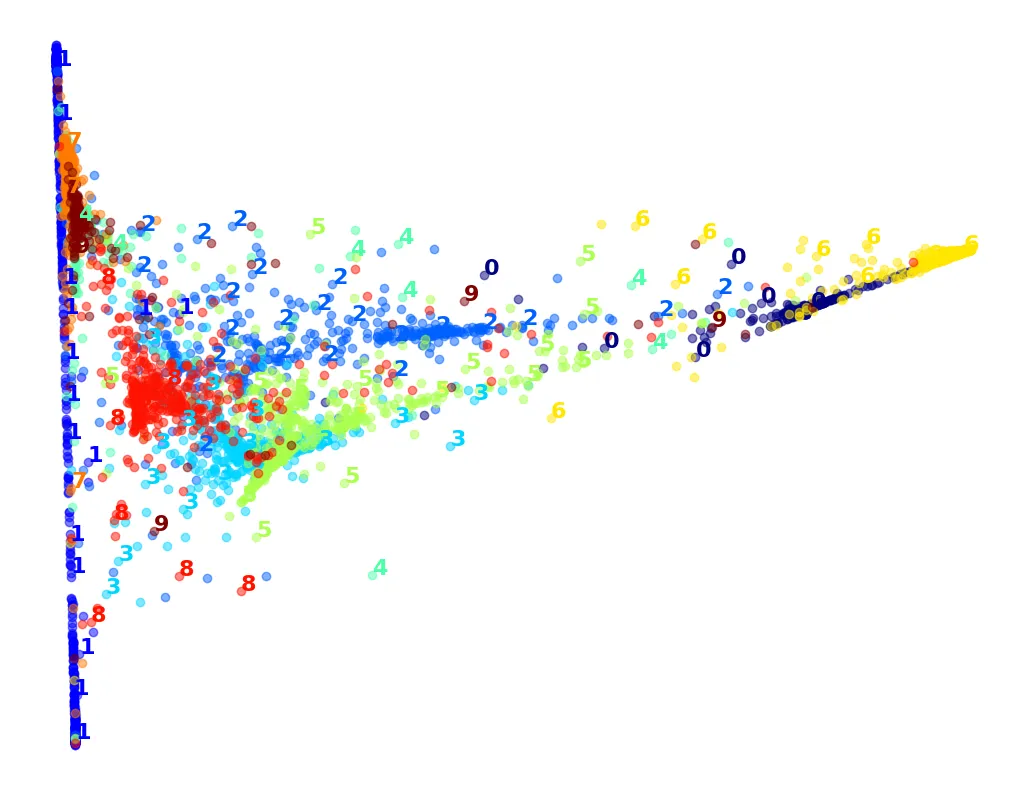

# MDS: Cảnh báo - Rất chậm (10-30 phút)
%time X_mds_reduced = MDS(n_components=2, normalized_stress=False, random_state=42).fit_transform(X_sample)
plot_digits(X_mds_reduced, y_sample)
plt.show()

CPU times: user 13min 37s, sys: 3min 44s, total: 17min 22s
Wall time: 13min 51s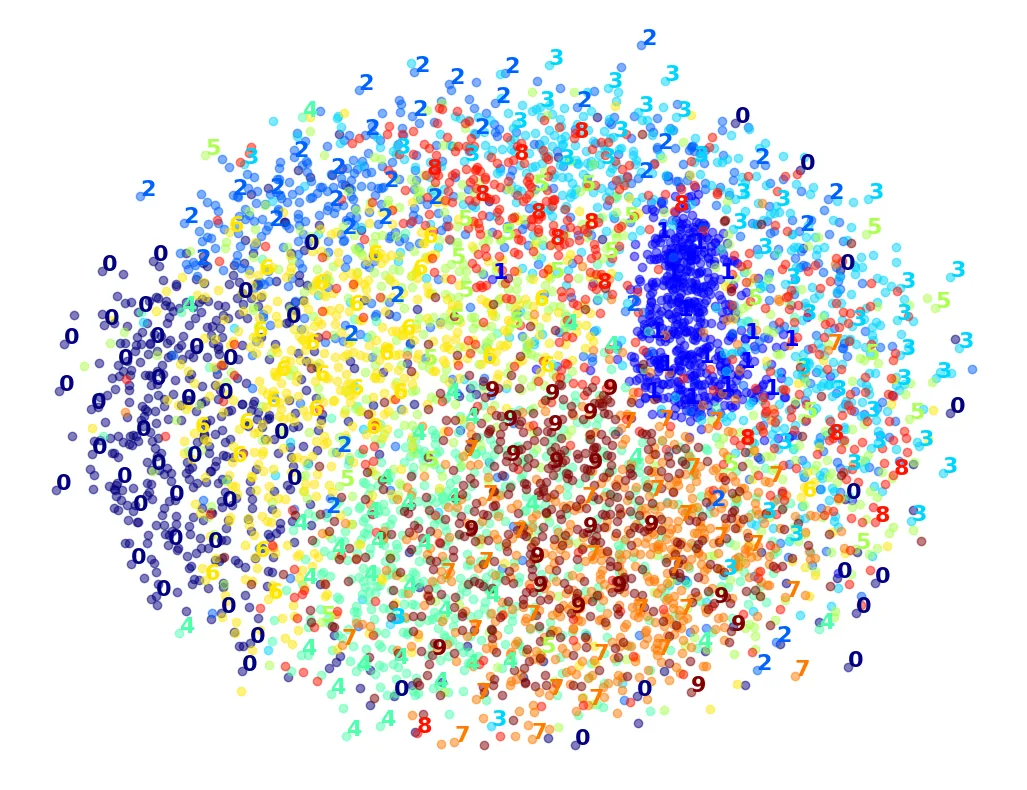

# PCA + MDS: Vẫn chậm và kết quả không cải thiện nhiều
pca_mds = make_pipeline(
    PCA(n_components=0.95, random_state=42),
    MDS(n_components=2, normalized_stress=False, random_state=42))
%time X_pca_mds_reduced = pca_mds.fit_transform(X_sample)
plot_digits(X_pca_mds_reduced, y_sample)
plt.show()

CPU times: user 13min 44s, sys: 3min 45s, total: 17min 29s
Wall time: 13min 51s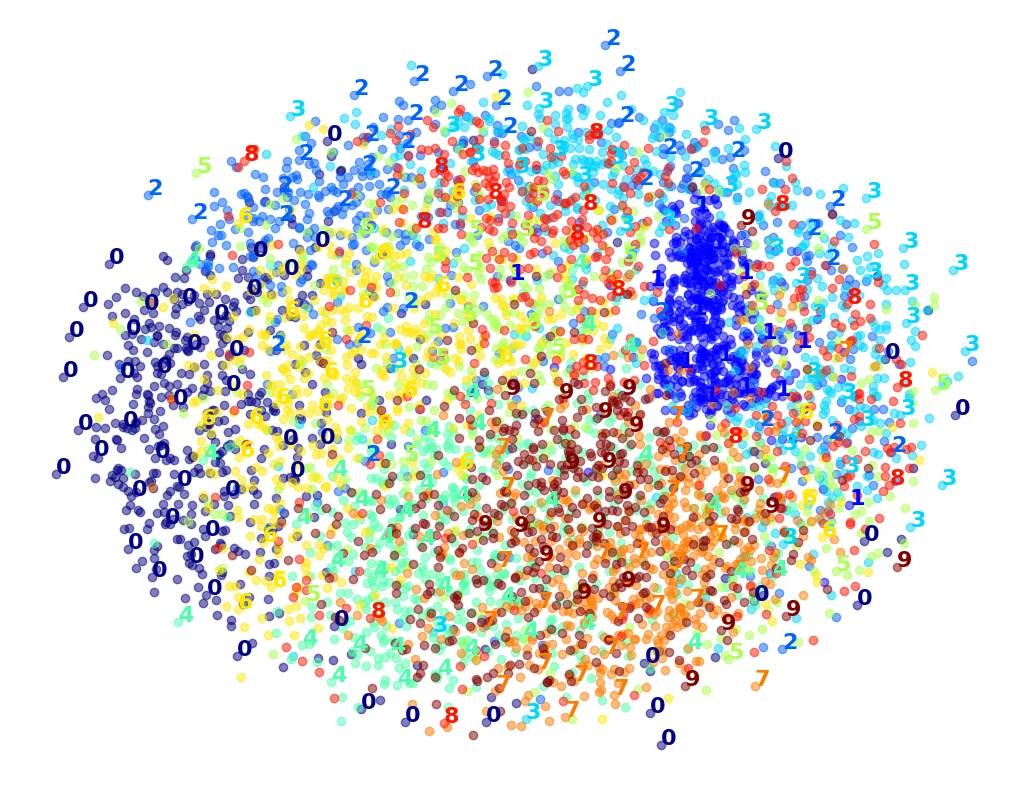

# LDA (Linear Discriminant Analysis): Rất nhanh, nhưng cũng bị chồng chéo
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

lda = LinearDiscriminantAnalysis(n_components=2)
%time X_lda_reduced = lda.fit_transform(X_sample, y_sample)
plot_digits(X_lda_reduced, y_sample, figsize=(12, 12))
plt.show()

CPU times: user 2.68 s, sys: 40.8 ms, total: 2.72 s
Wall time: 1.56 s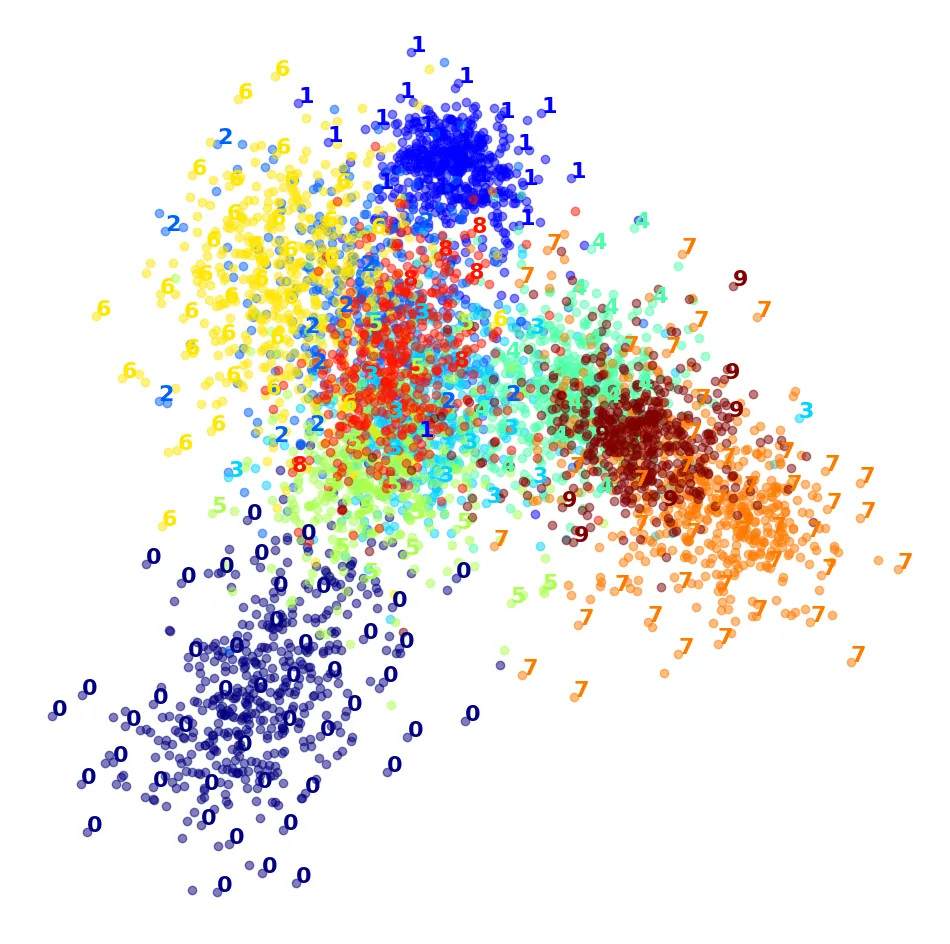

Kết luận: Trong cuộc thi trực quan hóa dữ liệu MNIST này, t-SNE rõ ràng là người chiến thắng về chất lượng hình ảnh, dù thời gian chạy lâu hơn PCA hay LDA.

Đó là toàn bộ nội dung của chương này. Hy vọng các bạn đã nắm được những kiến thức cốt lõi về Giảm chiều dữ liệu!